Elementary Concepts of Set Theory

More on Subsets

set of circles If a set A contains only elements of set B but not all of the elements of B, then

 

A is called the proper subset of B.

 

Mathematically, A ⊂ B.


Mathematics is the language for saying things precisely. Consider the statements:

Jack took apples from Jane

and

Jack took some apples from Jane

 

They are not the same statements. For instance, the later statement tells us that Jack has some but not all of Jane's apples. Hence, Jack's apples forms a proper subset of Jane's apples. On the other hand, the first statement does not tell us whether Jack took a few or all of Jane's apples. But, clearly Jack's apples are from Jane's. Thus, for this case Jack's apples forms a subset but not a proper subset of Jane's apples.

 

Thus,

In cases where set A contains only elements of set B but the stipulation that "elements in A are not all of the elements of B" is not necessary, then

 

A is called the subset of B.

 

Mathematically, A ⊆ B

 

In summary,

 
  • only elements of B
  • only elements of B
  • not all elements of B
A contains A ⊆ B A ⊂ B

 

 

Empty set Therefore, ⊂ (proper subset) is used when the added stipulation (of not all elements) is needed. In other words, ⊂ is used when precision is needed.

 

For instance,

 

set of purple circles (in A) = ϕ (empty set)

 

Hence, ϕ ⊂ A.


 

However, when we extend our understanding of empty sets and say that set of squares, set of spheres, set of polygons, set of apples etc. (in set A) are all empty set, i.e., = ϕ.

 

Then, ϕ ⊆ A.

Because, now ϕ represent arbitrary (null) set.

 

Note that ϕ ⊆ A also when A is an arbitrary set

 

 

Equal set eg The idea of subset (⊆) is made to use in defining equal sets

 

Two sets A and B are said to be equal if and only if (iff) A ⊆ B and B ⊆ A.

 

Thus A = B implies they define exactly the same elements.

 

Consider the statement,

Jack took apples from Jane

 

Let A represent the set of basket of apples (taken by Jack) and B be the set of Jane's basket.

 

For obvious reasons we can say, A ⊆ B.

 

And since after Jack takes the apples B = ϕ, we say B = ϕ ⊆ A.

 

Therefore, A = B in the sense that the basket contains the same apples.

 

In other words, one way to view this example is that A and B are the same basket of apples.

 

 

Unequal set eg On the other hand, if we consider the statement,

Jack took some apples from Jane

 

We see that, A ⊂ B and A ⊈ B & B ⊈ A.

 

Thus, A and B are not the same basket of apples.


 

set of circles Until now, all the examples have involved sets composed of items, i.e., individual sets.

 

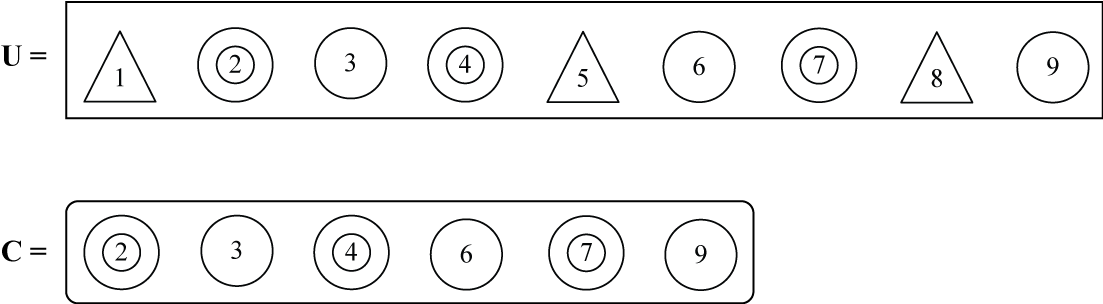
For the example of the set of circles, C, let us consider its subsets.


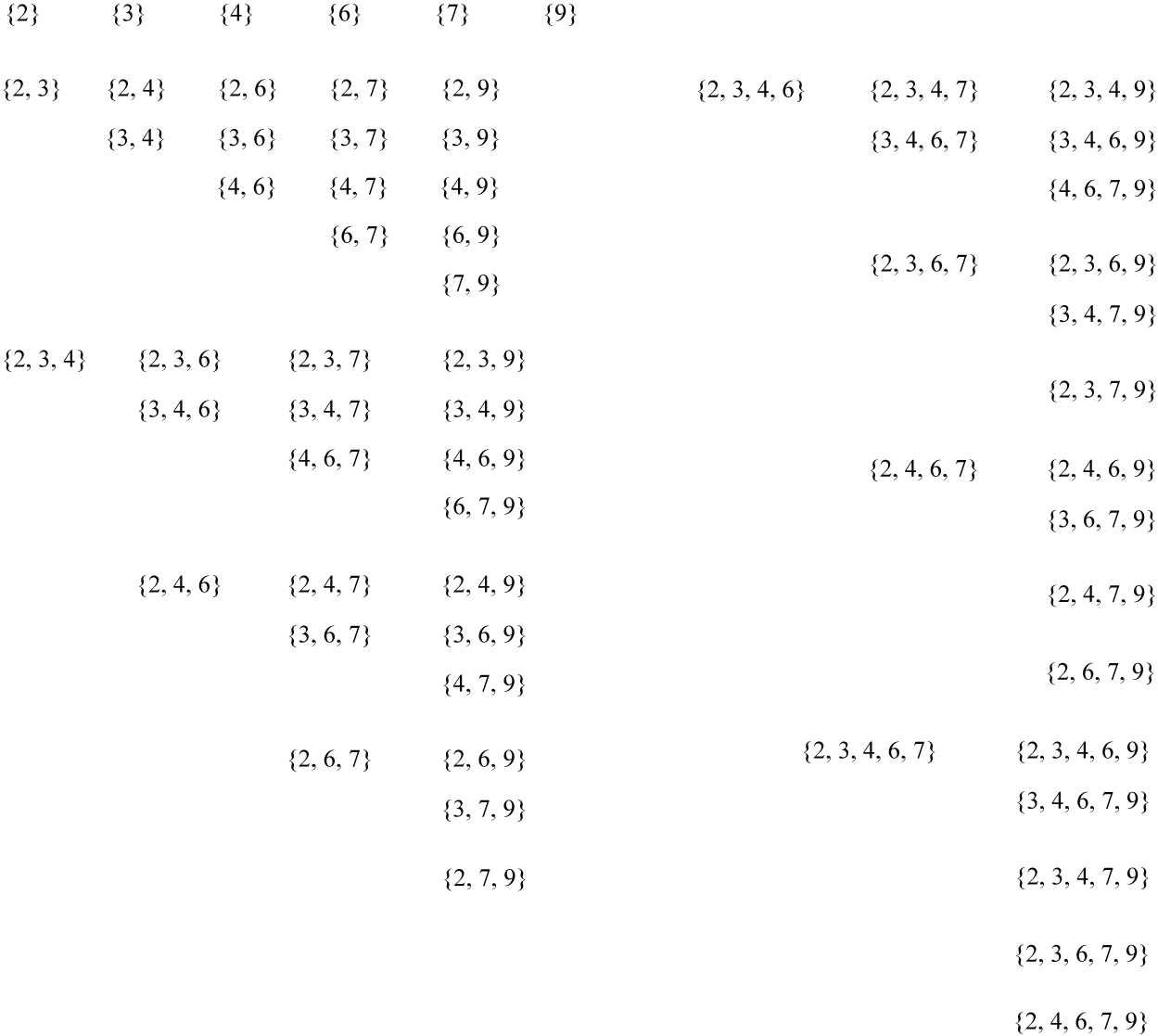subset of circles If X is the set composed of all the subsets of C, then

 

X is called the power set of C.

 

How many elements are in X?

This is same as, What are the total number of subsets of C ?

 

The answer is given by a simple formula.

 

If,

n : number of finite elements of C

 

Then,

X has 2n elements.

 

Thus, for our example 2n = 26 = 64. (Note: in addition to the 62 subsets on the right the other two subsets are ϕ and the set C itself)

 

Because the no. of elements in X is 2n, X is called the power set and is represented as, X = P(C)

 

 

Finally, if A and B are equal sets, i.e., A = B → A ⊆ B and B ⊆ A.

 

Then, P(A) = P(B).